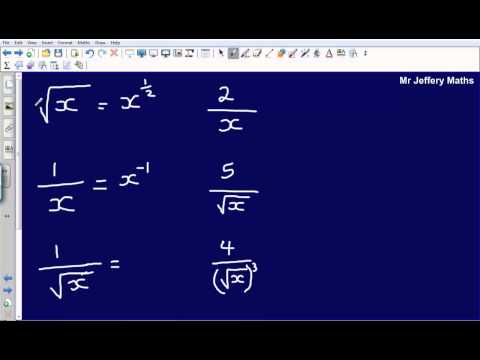
Hello and welcome to a video looking at more C1 indices. Now, at C1, it's just as important to be able to evaluate indices but also to be able to rewrite things that we see as part of equations as indices, particularly when we are differentiating. Here, I've got just six different examples which I'm going to rewrite as indices instead of what they've given us at the moment. So, here I've got the square root of x. Now, I could write the square root of x as an index, as x to the power of a half. One over x, how could I write that? Well, that's simply going to be x to the power of negative one. One over the square root of x, so I know that it's going to be a negative power and it's the square root. We saw here that the square root of x is x to the half. So, this is going to be x to the power of negative one-half. Here, we've got two over x. This I can write as 2x to the power of negative one. This one here, five over the square root of x, I can write as 5x to the negative one-half. And then lastly, this one here, 4 over the square root of x cubed, I can write as 4x to the negative three-halves. So, as I said at the beginning, it's just as important not only to be able to evaluate indices when they have a value, but it's just as important to be able to rewrite terms in an equation as indices, particularly when differentiating.
Award-winning PDF software





Video instructions and help with filling out and completing What Form 8815 Index