Where Form 8815 Index 2023-2024

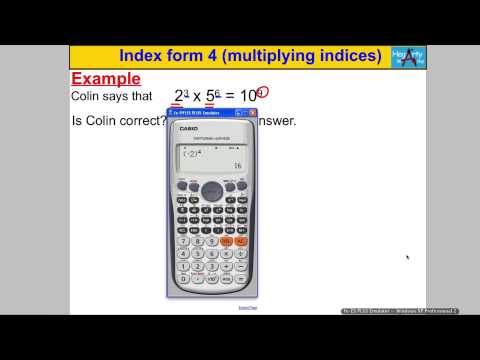
Hi there and welcome to another video from Hegarty Maths. If Mr. Haggerty here and this is our fourth video on index form. This time, we're going to be talking about multiplying indices and trying to generate a rule for that. So, to start with, I've introduced you to index form. How would a mathematician usually write - x - x - 7 x? Well, they would write 2^7. Now, I'm going to just break up this two in different ways. We know that when you're multiplying, multiplying is associative, so I can do it in any order I want. So let's just say I went like this: I did that on its own and then I did those multiplied. 2 here, that's 2 to the power of 1. These six 2's here are 2 to the power of 6. Obviously, I know my answer is 2 to the 7th. What if I did it in a different order? What if I said, "Right, I'm going to do them 2 and then I'm going to do them 5?" 2 squared multiplied by 2 to the power of 5 is, of course, 2 to the 7th. What if I broke it up in a different order again? What if I said, "I don't know, like this?" and I said, "Right, 2 to the 4, therefore multiplied by 2 to the 3." Well, obviously, that's 2 to the 7th. And I could break it up in any way I want. So let's say I said, "I don't know, I did these two and then I did these three and then I did these two last." So that would be 2 squared multiplied by 2 cubed multiplied by 2 squared. And I know the answer's 2 to the 7. Now, can you spot what I'm trying to...