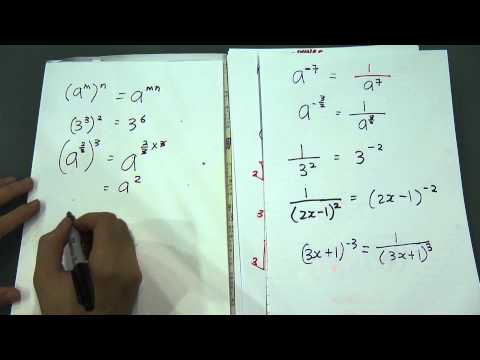Who Form 8815 Index 2024-2025

Okay, today I'm going to teach about some basic laws of indices or exponents. Okay, all right, for this section on indices, there are a few very important laws. The first law is called the power of a power law. It states that when you have a power of a number raised to another power, you multiply the exponents, so a raised to the power of m raised to the power of n is equal to a raised to the power of m multiplied by n. For example, (2^7)^e would be equal to 2^(7e), which can be simplified to 2^(15). Another important law is the division law. It states that when you have a power divided by another power, you subtract the exponents. So a raised to the power of m divided by a raised to the power of n is equal to a raised to the power of m minus n. For example, 2^8 divided by 2^3 would be equal to 2^(8-3), which simplifies to 2^5. The same rules apply to other laws of indices as well. For example, with fractional exponents, the top number represents the power, and the bottom number represents the root. So M^(3/2) can also be written as the square root of M cubed. For example, 7^(2/3) can be written as the cube root of 7 squared. Similarly, when you see expressions like square root(2x+1), you can also write it as (2x+1)^(1/2). Let's consider another example: cube root(4x-7) can be written as (4x-7)^(1/3). There might be instances where you encounter more complex expressions, such as square root(4x-7) squared. In this case, you would square the entire expression, resulting in (4x-7)^(2/2). To simplify the expression further, note that 2/2 is equal to 1. So, the simplified form is (4x-7)^(1). Now let's address what happens when you have negative exponents. When you...